8 Discussion 06: Chance & Models (from Fall 2025)

8.0.1 Contact Information

Name	Wesley Zheng
Pronouns	He/him/his
Email	wzheng0302@berkeley.edu
Discussion	Wednesdays, 12–2 PM @ Etcheverry 3105
Office Hours	Tuesdays/Thursdays, 2–3 PM @ Warren Hall 101

Contact me by email at ease — I typically respond within a day or so!

8.0.2 Announcements

Announcements

Project 01 is due Friday at 5 PM. Submit by Thursday at 5 PM for extra credit.
Only one student per group should submit and add the others on Pensieve.
Students needing midterm accommodations should send DSP letters as soon as possible.

Project Parties:

9/30, 6–8 PM, SOCS 175 (location TBD)
10/1, 6–8 PM, Evans B6

8.1 Marble Madness

8.1.1 (a)

Tiffany has a bag with three marbles. One marble is orange, and the other two are purple. For each round of a game, she draws from the bag 10 times with replacement. She wins the round by drawing at least one orange marble.

Write a function to simulate one round of Tiffany’s game. The function should return True if she wins and False if she loses.

Code

from datascience import *
import numpy as np
%matplotlib inline

def one_round():
  bag = ____________________________________________________
  one_sim = ________________________________________________
  num_orange = _____________________________________________
  return ___________________________________________________

Answer

def one_round():
  bag = make_array('purple', 'purple', 'orange')
  one_sim = np.random.choice(bag, 10)
  num_orange = sum(one_sim == 'orange')
  return num_orange >= 1

Instead of sum, students can also use np.count_nonzero(). They can also use sample_proportions with probabilities ($\frac{2}{3}$, $\frac{1}{3}$).

Working with Probability and Functions

Defining a function that simulates one round is like defining a function to calculate a test statistic.

Start by defining the bag (population):

make_array("orange", "purple", "purple")

Use == to check which marbles are orange.
Use sum or np.count_nonzero to count how many orange marbles are in a sample.

one_round()

True

8.1.2 (b)

Finish the following code to help Tiffany simulate 100 rounds of the game and assign the variable win_proportion to the proportion of rounds she wins.

count = 0
for _____________________________________________:
  if ________________________________________________:
    ________________________________________________________
win_proportion = _______________________________________________

Answer

count = 0
for i in np.arange(100):
    if one_round():
        count = count + 1
win_proportion = count / 100

win_proportion

1.0

Note that the line “if one_round()” works by incrementing the count variable when one_round() evaluates to True (and will not if one_round() evaluates to False).

8.1.3 (c)

For any one draw, what is the probability that Tiffany draws a purple marble?

Answer

$P(Draw\:a\:purple\:marble) = \frac{2}{3}$

8.1.4 (d)

For any individual round, what is the probability that Tiffany loses?

Answer

Using the multiplication rule:

$P(Tiffany\:loses\:one\:round) = P(draw\:10\:purples) = P(purple)^{10} = (\frac{2}{3})^{10}$

8.1.5 (e)

For any individual round, what is the probability that Tiffany wins?

Answer

Using the complement rule:

$P(Tiffany\:wins\:one\:round) = 1 - P(Tiffany\:loses\:one\:round) = 1 - (\frac{2}{3})^{10}$

Example: Probability of Tiffany Winning

Probability Tiffany loses: she must draw all purple marbles.
\[ P(\text{all purple}) = \left(\frac{2}{3}\right)^{10} \]
Probability Tiffany wins:
\[ 1 - \left(\frac{2}{3}\right)^{10} \]

8.2 Flip Flop

Brandon is flipping a coin. He thinks it is unfair, but is not sure. He flips it 10 times and gets heads 9 times. He wants to determine whether the coin was actually unfair, or whether the coin was fair and his result of 9 heads in 10 flips was due to random chance.

8.2.1 (a)

What is a possible model that he can simulate under?

Answer

A possible model that you could simulate under is that on each flip, there is a 50% chance that the coin lands heads and a 50% chance that the coin lands tails. Any difference is due to chance.

If you are more familiar with probability: The heads are like independent and identically distributed draws at random from a distribution in which 50% are Heads and 50% are Tails.

8.2.2 (b)

What is an alternative model for Brandon’s coin? You do not necessarily have to be able to simulate under this model.

Answer

An alternative model that Brandon might suggest is that the coin is unfair, and that the difference in the observed data is due to something other than just chance. We would not be able to simulate under this model because the statement “the coin is unfair” is not very specific (we can ask questions like “How unfair?” or “Biased towards heads or tails?”).

8.2.3 (c)

What is a good test statistic that you could compute from the outcome of his flips? Calculate that statistic for your observed data. Hint: If the coin was unfair, it could either be biased towards heads or biased towards tails.

Answer

A good test statistic is the absolute difference between the number of heads we observe and the expected number of heads (5). Our observed test statistic is $$9 - 5$$ = 4. Notice that this statistic is large for both a large number of heads, as well as a small number of heads.

We could also use proportions as our test statistic, i.e., $\vert$ proportion of heads - 0.5 $\vert$.

8.2.4 (d)

Complete the function flip_ten, which takes no arguments and does the following:

Simulates flipping a fair coin 10 times
Computes the simulated statistics, based on the one chosen in the previous question

def flip_ten():
  faces = make_array("Heads", "Tails")
  flips = ___________________________________________________________
  num_heads = _______________________________________________________
  return ____________________________________________________________

Answer

def flip_ten():
    faces = make_array("Heads", "Tails")
    flips = np.random.choice(faces, 10)
    num_heads = np.count_nonzero(flips == "Heads")
    return abs(num_heads - 5)

flip_ten()

8.2.5 (e)

Complete the code below to simulate the experiment 10000 times and record the statistic computed in each of those trials in an array called simulated_stats.

trials = _____________________________________________________________
simulated_stats = ____________________________________________________
for _________________________________________:
  one_stat = ________________________________________
  _______________ = _________________________

How Simulation Is Structured

Steps for simulating:
1. Define a function that simulates once and computes one test statistic.
2. Run a for-loop that:
  - Calls this function.
  - Stores results in an array.
Key reminder: sample size ≠ number of repetitions.
This structure shows up often and is worth practicing.

Answer

trials = 10000
simulated_stats = make_array()
for i in np.arange(trials):
    one_stat = flip_ten()
    simulated_stats = np.append(simulated_stats, one_stat)

simulated_stats

array([ 1.,  0.,  0., ...,  2.,  0.,  0.])

8.2.6 (f)

Suppose we performed the simulation and plotted a histogram of simulated_stats. The histogram is shown below.

Code

Table().with_columns('Absolute Differences', simulated_stats).hist("Absolute Differences", bins = np.arange(11))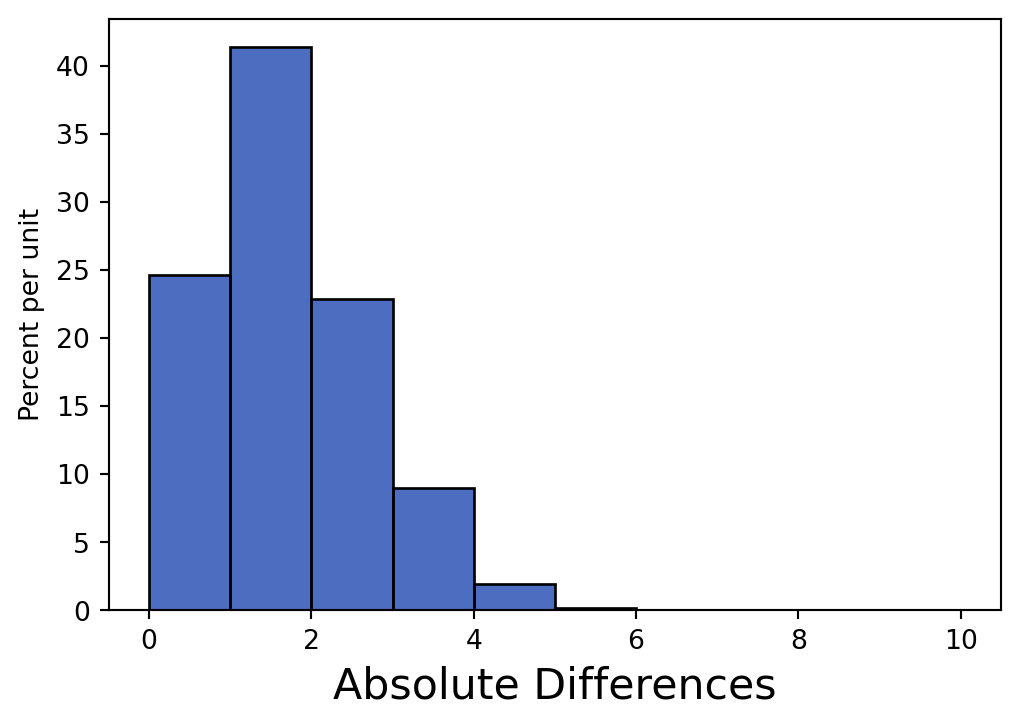

Is our observed statistic from (c) consistent with the model we simulated under?

Answer

No, the observed statistic is not consistent with the model we simulated under. If we look for the observed statistic (4), we will see that it rarely ever happened in our simulation; most of the statistics generated in our simulations were in the range [0, 2]. Therefore, we would say that it is inconsistent with the model we simulated under.

8.3 Tickets

(Spring 2017 Midterm Question 3)

8.3.1 (a)

A basket of 10 colored tickets contains 1 blue, 1 gold, 4 green, and 4 red tickets. If you draw 6 tickets uniformly at random with replacement, what is the chance that you draw at least one that is either blue or gold? Write your answer as a Python expression that computes the result exactly (no simulation).

Answer

1 - 0.8 ** 6

0.7378559999999998

8.3.2 (b)

The roll function draws an empirical histogram of the number of results that are $k$ or larger, when $n$ fair 6-sided dice are rolled. For example, if $k$ = 5, $n$ = 3, and rolling three dice results in the faces $\{6, 4, 5\}$, then two of the three dice are 5 or larger (the 6 and the 5). Fill in the blanks to complete its implementation.

def roll(k, n, trials):
  """Repeatedly roll `n` dice `trials` times and check how many results are `k` or larger."""
  outcomes = make_array()
  possible_results = _______________________________________
  for i in _________________________________________________:
    rolls = _____________________________________________________
    outcomes = __________________________________________________
  Table().with_column("Outcomes", outcomes).hist(bins=np.arange(30))

Answer

def roll(k, n, trials):
  """Repeatedly roll n dice and check how many results are k or larger."""
  outcomes = make_array()
  possible_results = np.arange(1, 7)
  for i in np.arange(trials):
    rolls = np.random.choice(possible_results, n)
    outcomes = np.append(outcomes, np.count_nonzero(rolls >= k))
  Table().with_column('Outcomes', outcomes).hist(bins = np.arange(30))

roll(5, 30, 1000)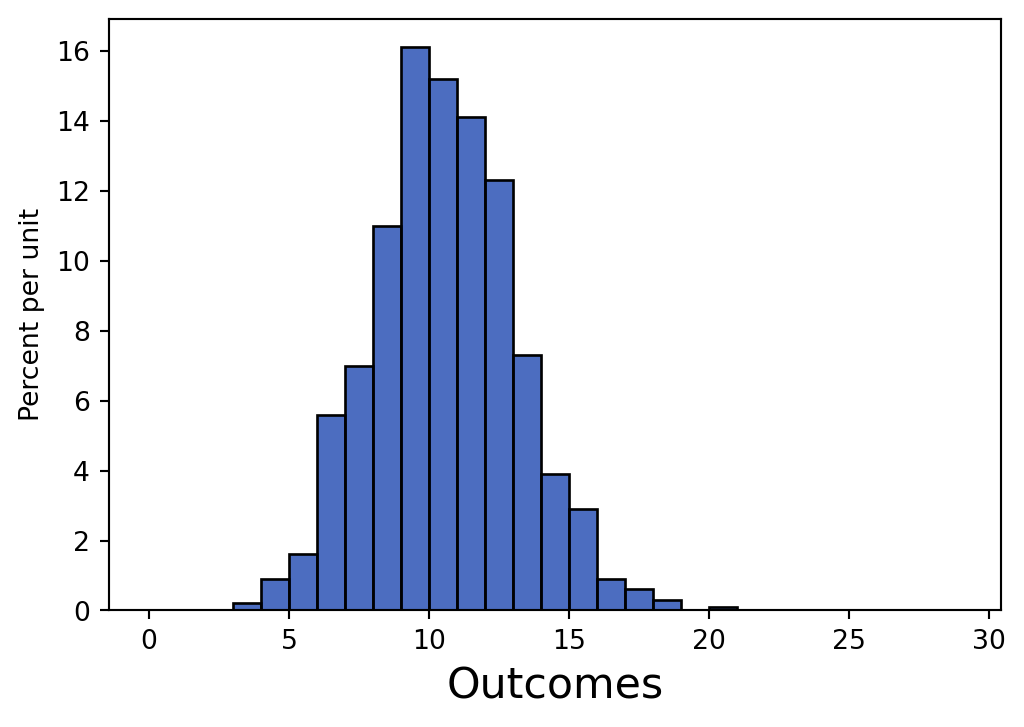

8.3.3 (c)

Assume roll is implemented correctly for the below questions.

Code

roll(6, 30, 5000)
roll(4, 30, 50)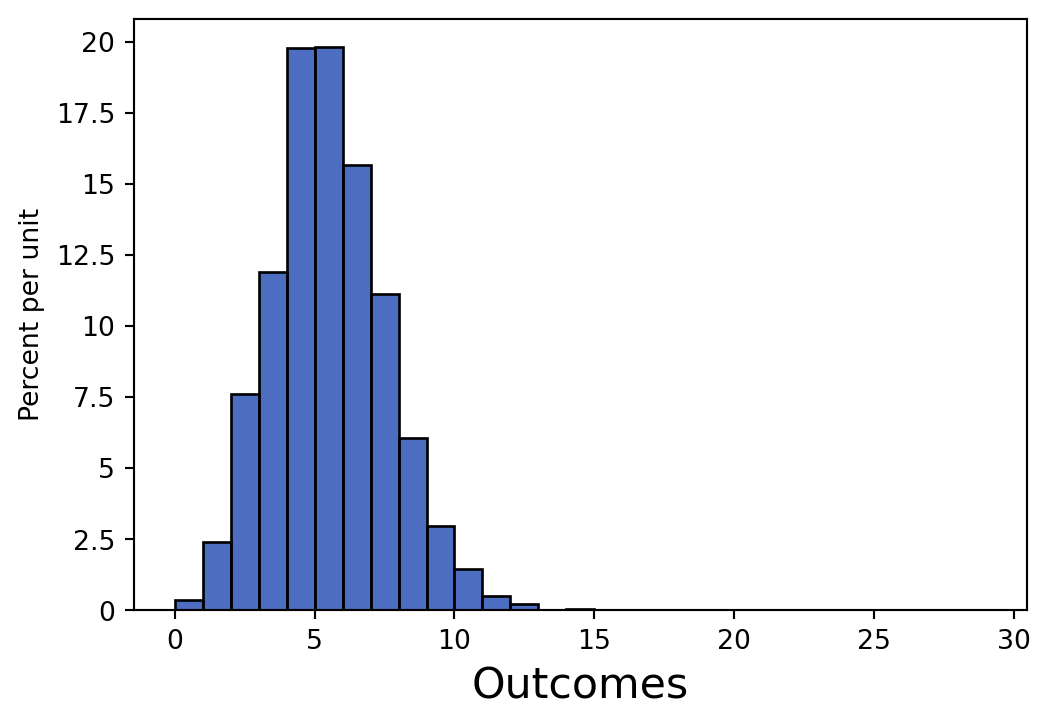

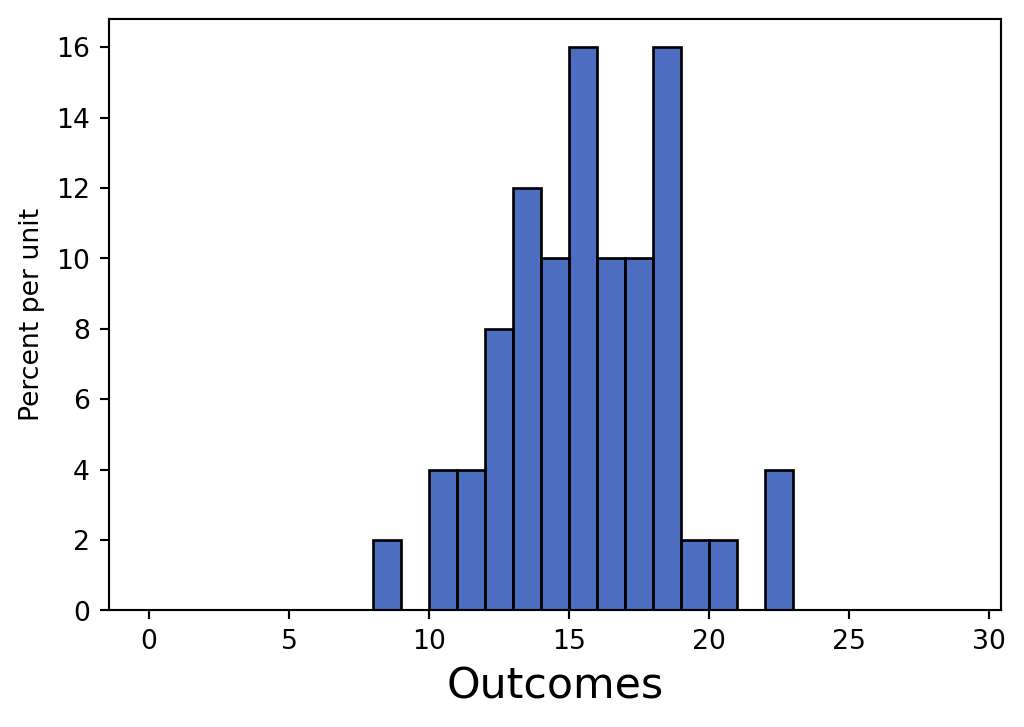
8.3.3.1 (i)

Which expression generates the first histogram?

roll(4, 30, 5000) roll(6, 30, 5000) roll(4, 30, 50) roll(6, 30, 50)

Answer

roll(6, 30, 5000)

8.3.3.2 (ii)

Which expression generates the second histogram?

roll(4, 30, 5000) roll(6, 30, 5000) roll(4, 30, 50) roll(6, 30, 50)

Answer

roll(4, 30, 50)