Code
import numpy as np
from datascience import *
%matplotlib inline
amounts = np.random.normal(loc=2.5, scale=1, size=150)
amounts = np.clip(amounts, 0.5, 7)
water = Table().with_columns(
"amount", amounts
)11 Discussion 09: The Bootstrap (from Fall 2025)
11.0.1 Contact Information
| Name | Wesley Zheng |
| Pronouns | He/him/his |
| wzheng0302@berkeley.edu | |
| Discussion | Wednesdays, 12–2 PM @ Etcheverry 3105 |
| Office Hours | Tuesdays/Thursdays, 2–3 PM @ Warren Hall 101 |
Contact me by email at ease — I typically respond within a day or so!
11.0.2 Announcements
11.1 Mid-Semester Check In
Congrats on finishing the midterm!
What has been your favorite topic, assignment, lecture, or anything so far with the first half of the class done? Please leave any comments you have about the content and any feedback for your TA here. Tear this page off and fold it so it is anonymous.
Additionally, if you have any concerns about your performance in the class so far, feel free to bring it up with your TA in person, or via email.
11.2 The Bootstrap
NoteNote
Setup
We want to be able to produce an estimate of a particular population parameter of interest, say the median. However, we know that if we had gotten a different sample, then our estimate of the population median could have also been different.
Main Objective
If we were satisfied with our sample, we could simply take the statistic of the sample and call it the prediction for the population median. Even though this is a valid approximation method, we want to use the method of the bootstrap to generate a range of values for which we believe our population parameter falls into.
Method
Ideally, we would be able to take more samples from the population and find estimates for the population parameter in all of these samples. However, we are usually not able to resample from the original population due to resource constraints, necessitating the process of the bootstrap.
- Given a large, simple random sample of a population, resample from the original sample with replacement. Generate many resamples with the same sample size as the original sample.
- Calculate the statistic for each resample and store it in a collection array, as we saw in the case of hypothesis testing.
- Repeat steps 1–2 multiple times to obtain an empirical distribution of your estimate.
11.2.1 (a)
When we conduct a bootstrap resample, what size resample should we draw from our sample? Why?
Answer
The resample should have the same sample size as our original sample. This is because our original estimate of some parameter is based on a certain sample size. If we changed the sample size, the distribution and variability of the estimate would change.11.2.2 (b)
Why do we need to resample from our sample with replacement?
Answer
If we do not sample with replacement, then we will get the same exact sample every time! By sampling with replacement, this allows us to simulate different resamples from the sample.11.2.3 (c)
When we conduct a bootstrap resample, what is the underlying assumption/reasoning for resampling from our sample? Why does it work?
Answer
The underlying assumption is that our sample looks similar to our population — that is, the sample is representative of what the population looks like. The validity of the bootstrap is based on this assumption because if the sample is unrepresentative of the population, we do not actually end up with a good picture of what range of values our estimate could take on.11.3 Thirsty
11.3.1 (a)
Warm Up: What is the difference between a parameter and a statistic? Which of the two is random?
Answer
A parameter is a property of the population, so it is fixed and does not change. On the other hand, we calculate statistics from samples which are often random. Typically, we use statistics in order to estimate population parameters.You are interested in investigating the liters of water consumed every day by UC Berkeley students. In particular, you want to study the proportion of students drinking less than 3 liters of water per day. You contact 150 random students from the directory and obtain the amounts of water each one of them drinks, storing them in the table water. The table has 1 column, amount, which stores the number of liters of water drunk by each student.
11.3.2 (b)
What is the parameter and what is the statistic in this scenario?
Answer
Parameter: The proportion of UC Berkeley students who drink less than 3 liters of water per day.
Statistic: The proportion of students in the sample who drink less than 3 liters of water per day.11.3.3 (c)
Write a line of code to calculate the proportion of students in your sample who drank less than 3 liters of water per day.
Answer
np.mean(water.column("amount") < 3)0.6733333333333333411.3.4 (c)
Write a line of code to perform a single bootstrap resample of the data stored in the water table.
Answer
water.sample(water.num_rows, with_replacement = True)| amount |
|---|
| 2.18193 |
| 2.76407 |
| 2.40837 |
| 2.42827 |
| 1.74703 |
| 2.12026 |
| 2.75679 |
| 2.98493 |
| 2.8872 |
| 1.94332 |
... (140 rows omitted)
Alternatively, given the default values of the arguments, you may simply write
water.sample()| amount |
|---|
| 2.98493 |
| 2.38245 |
| 1.24443 |
| 2.98493 |
| 2.67321 |
| 3.06458 |
| 2.50129 |
| 2.75679 |
| 2.20771 |
| 4.47429 |
... (140 rows omitted)
11.3.5 (e)
Fill in the following blanks to conduct 10,000 bootstrap resamples of your data, calculating the proportion of students in each resample that drink less than 3 liters of water per day, then plotting the distribution of those proportions using an appropriate visualization.
proportions = _______________
for i in _______________:
resampled_table = ________________________________
resampled_statistic = __________________________
proportions = _____________________________
proportions_table = Table().with_column("Resampled proportions", proportions)
proportions_table._______________Answer
proportions = make_array()
for i in np.arange(10000):
resampled_table = water.sample(water.num_rows, with_replacement=True)
resampled_statistic = np.mean(resampled_table.column("amount") < 3)
proportions = np.append(proportions, resampled_statistic)
proportions_table = Table().with_column("Resampled proportions", proportions)
proportions_table.hist("Resampled proportions")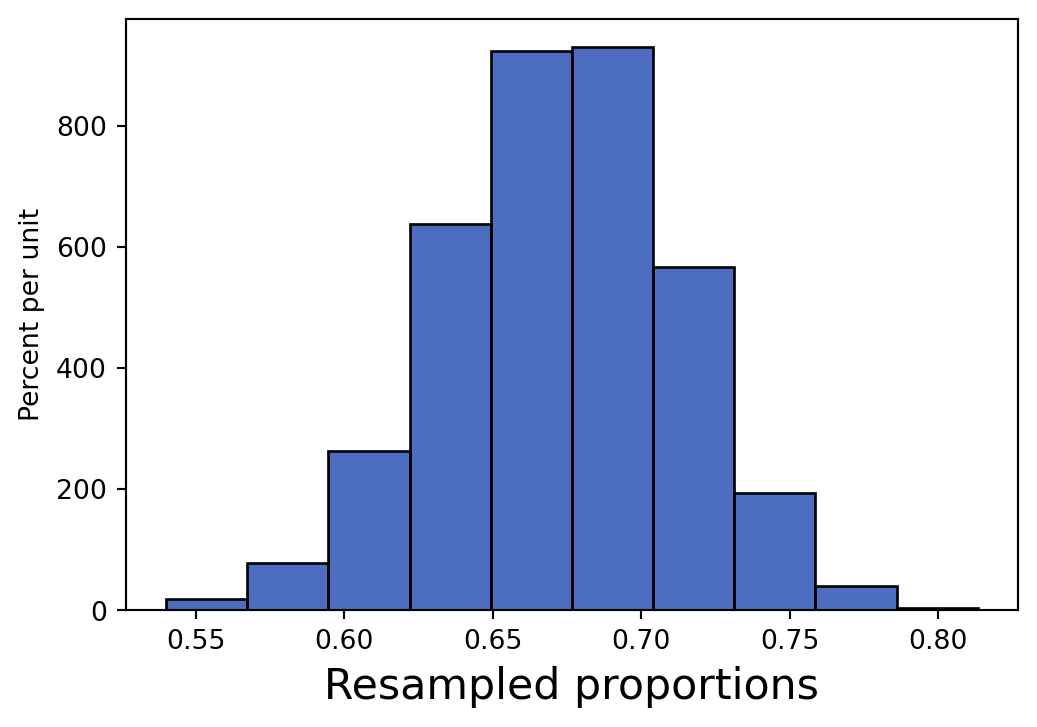
11.4 Tennis Time
Ciana is interested in exploring the heights of women’s tennis players. She has collected a sample of 100 heights of professional women’s tennis players and wants to use this sample to estimate the true interquartile range (IQR) of all heights of professional women’s tennis players.
We define the interquartile range (IQR) as:
Code
heights = np.random.normal(loc=175, scale=7, size=100)
tennis = Table().with_columns(
"Height (cm)", heights
)11.4.1 (a)
In order to construct a 99% confidence interval for the IQR, what should our upper and lower endpoints be in terms of percentiles?
Answer
Our lower endpoint should be the 0.5th percentile and the upper endpoint should be the 99.5th percentile.
11.4.2 (b)
Define a function ci_iqr that constructs a 99% confidence interval for the IQR and returns an array containing the left endpoint and right endpoint of the 99% confidence interval in that order. The function takes in the following arguments:
tbl: A one-column table consisting of a random sample from the population; you can assume this sample is large.reps: The number of bootstrap repetitions.
To find the 25th and 75th percentile of an array, you can use the percentile function.
Fill in the blanks and then provide the full solution.
def ci_iqr(tbl, reps):
stats = _______________
for ________________:
resample_col = ________________________________
new_iqr = _________________________________
stats = __________________________________
left_end = _______________
right_end = ______________
return ______________Answer
def ci_iqr(tbl, reps):
stats = make_array()
for i in np.arange(reps):
resample_col = tbl.sample().column(0)
new_iqr = percentile(75, resample_col) - percentile(25, resample_col)
stats = np.append(stats, new_iqr)
left_end = percentile(0.5, stats)
right_end = percentile(99.5, stats)
return make_array(left_end, right_end)ci_iqr(tennis, 100)array([ 4.39664965, 10.81363711])11.4.3 (c)
Say Ciana recruited 500 of her friends to perform the same bootstrapping process she did. In other words, each of her friends drew a large, random sample of 100 heights from the population of professional women’s tennis players and constructed their own 99% confidence intervals.
11.4.3.1 (i)
Approximately how many of these CIs do we expect to contain the actual IQR for the heights of professional women’s tennis athletes?
Answer
We interpret a 99% confidence interval to mean that we are 99% confident in the process used to construct that given interval. In other words, 99% of the time we use this process we expect to construct an interval that contains the true population parameter.
Since we have 500 CIs, each at a 99% confidence level, we find that since \(500 \cdot (0.99) = 495\), we expect to have 495 of these CIs containing the actual IQR of heights.11.4.3.2 (ii)
Note how in this example, we obtain different random samples from the population for each confidence interval, and then re-sample from each to produce a confidence interval.
Why each person not just re-use the same original sample? Why is this distinction important?
Answer
Recall the “confidence” is the confidence in the process, and it is the process of drawing new, independent samples from the population and building a confidence interval for each. The re-sample is conditioned on the single sample you obtained, and models only the variability of that sample – we would just be constructing the same CI over and over.11.4.3.3 (iii)
Ciara decided to do this process again, but this time with only 50 of her friends. Would the number of CIs that contain the actual IQR be more or less close to the expected number of CIs, compared to her results with 500 friends?
Answer
It would be less close, by law of large numbers (higher variability).11.4.4 (d)
Ciara now decides to perform a hypothesis test, with the null hypothesis that the true IQR is q.
11.4.4.1 (i)
How could Ciara perform this using her confidence intervals? Discuss the duality of confidence intervals and hypothesis testing.
Answer
The confidence interval describes the region for which we can be 99% confident that it contains the true population parameter. This describes exactly the error of the p-value cutoff.
The decision rule for a hypothesis test testing whether the IQR is q could therefore be
- reject if s is not contained in the 99% CI
- fail to reject otherwise
11.4.4.2 (ii)
If Ciara conducted a two-tailed hypothesis test (e.g. her alternative was “the IQR is not q”), what p-value cutoff would she choose if she used her confidence intervals?
Answer
1%, since we construct 99% confidence intervals, and we look at both tails.11.4.4.3 (iii)
If Ciara conducted a one-tailed hypothesis test (e.g. her alternative was “the IQR is greater than q”), what p-value cutoff would she choose if she used her confidence intervals?
Answer
The effective cutoff should be 0.5%, since we construct 99% confidence intervals, but only look at one tail. This is true since the confidence intervals we generate will have equal tails*, and therefore the same probability, so we can halve the tail region.
Typically, we would choose a p-value cutoff first, such as of 1% and then construct 98% confidence intervals to determine the outcome of the test. For the purposes of this question, we used the same confidence interval for both part (v) and part (vi).
*Note: bootstrapped percentile confidence intervals have equal tails, but may not be symmetric. Confidence intervals generated in other ways, not taught in Data 8, may not have equal tails.